Statistical Regression Analysis

T. Dhasaratharaman*

Statistician, Kauvery Hospitals, India

*Correspondence: Tel.: +91 90037 84310; email: [email protected]

Definition

The Regression Analysis is a technique of studying the dependence of one variable (called dependent variable), on one or more variables (called explanatory variable), with a view to estimate or predict the average value of the dependent variable in terms of the known or fixed values of the independent variables.

Regression analysis is used to find how one set of data relates to another.

This can be particularly helpful where we want to use one measure as a proxy for another – for example, a near-patient test as a proxy for a lab test.

Interpretation

A regression line is the “best fit” line through the data points on a graph.

The regression coefficient gives the “slope” of the graph, in that it gives the change in value of one outcome, per unit change in the other.

Example

Consider the graph shown in previous section. A statistician calculated the line that gave the “best fit” through the scatter of points

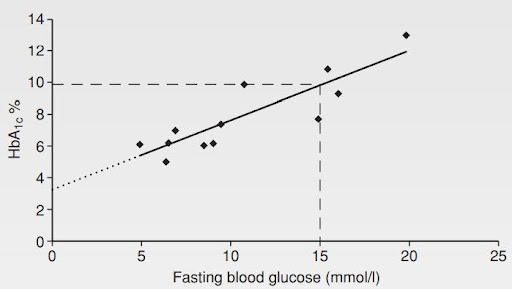
The line is called a “regression line”.

To predict the HbA1c for a given blood glucose the nurse could simply plot it on the graph, as here where a fasting glucose of 15 predicts an HbA1c of 9.95.

This can also be done mathematically. The slope and position of the regression line can be represented by the “regression equation”:

HbA1c = 3.2 + (0.45 × blood glucose).

The 0.45 figure gives the slope of the graph and is called the “regression coefficient”.

The “regression constant” that gives the position of the line on the graph is 3.2: it is the point where the line crosses the vertical axis.

Try this with a glucose of 15:

HbA1c =3.2+(0.45×15) = 3.2+6.75=9.95

This regression equation can be applied to any regression line. It is represented by:

y = a + bx

To predict the value y (value on the vertical axis of the graph) from the value x (on the horizontal axis), b is the regression coefficient and a is the constant.

Other types of regression

The example above is a “linear regression”, as the line that best fits the points is straight. Other forms of regression include:

Logistic regression: This is used where each case in the sample can only belong to one of two groups (e.g. having disease or not) with the outcome as the probability that a case belongs to one group rather than the other.

Poisson Regression: It is mainly used to study waiting times or time between rare events.

Cox proportional hazards regression model: It is used in survival analysis where the outcome is time until a certain event.

Caution

Regression should not be used to make predictions outside of the range of the original data. In the example above, we can only make predictions from blood glucoses which are between 5 and 20.

Regression vs correlation

Regression and correlation are easily confused.

Correlation measures the strength of the association between variables.

Regression quantifies the association. It should only be used if one of the variables is thought to precede or cause the other.

Mr. T. Dhasaratharaman

Statistician

Statistical Regression Analysis

Statistical Regression Analysis

Journals